Prawo Mandelbrota-Zipfa-Rényiego
Marek Czachor (Politechnika Gdańska)
Jeżeli weźmiemy dowolny, wystarczająco długi tekst (lub korpus tekstów) i policzymy, ile razy występują w nim poszczególne słowa, to zaobserwujemy ciekawą prawidłowość: jeżeli tylko mamy do czynienia z językiem naturalnym, wykres przedstawiający ułożenie wyrazów w malejącym porządku częstotliwości zawsze przyjmie taki sam kształt. Jest to tzw. rozkład Zipfa (Zipf, 1935).
Poniższe trzy wykresy przedstawiają typowe dane korpusowe (Szekspir i Dickens; wykresy górne) oraz czas wiązania się tlenku węgla (czadu) z mioglobiną, białkiem odpowiedzialnym za działanie naszych mięśni (dla różnych temperatur; wykres dolny).
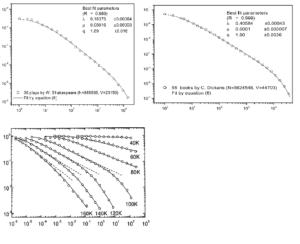
Podobieństwo jest oczywiste, co sugeruje istnienie ogólnej zasady statystycznej wykraczającej poza językoznawstwo czy biologię molekularną. Na każdym z powyższych wykresów można wyróżnić trzy obszary: lewy (poziomy; pierwsze podgięcie w dół), środkowy (fragment linii prostej) i prawy (drugie podgięcie w dół). Odcinek środkowy opisywany jest przez klasyczne prawo Zipfa (Zipf, 1935). Odcinek pierwszy i drugi są łącznie opisywane przez prawo Zipfa-Mandelbrota (Mandelbrot, 1965). Nas interesuje obszar trzeci, a właściwie prawo, które obejmowałoby wszystkie trzy obszary, ponieważ powszechnie stosowane formuły nie tłumaczą, dlaczego linia wykresu „załamuje się” u dołu. Co więcej, nie chodzi nam o po prostu odgadnięcie pewnej formuły matematycznej, lecz o jej wyprowadzenie z zasad ogólnych.
Okazuje się (Czachor-Naudts, 2002), że „przyczyną pierwszą” może być jedna z podstawowych zasad termodynamiki, mianowicie proces osiągania tzw. równowagi termodynamicznej – zjawisko znane nam z życia codziennego jako stygnięcie niedopitej kawy. W przypadku prawa Zipfa „sztuczka” polega na odpowiednim zdefiniowaniu wartości średniej, co ostatecznie prowadzi do entropii Rényiego (Rényi, 1960). Pojęcie entropii odgrywa kluczową rolę zarówno w teorii termodynamiki (Clausius, 1865), jak i w teorii informacji (Shannon, 1948). W obu tych teoriach odnosi się ono do poziomu niepewności lub rozproszenia układu.
Można więc mówić o tytułowym prawie Mandelbrota-Zipfa-Rényiego, które unifikuje wszystkie trzy obszary danych (lewy: Mandelbrot, środkowy: Zipf, prawy: Rényi). Prawo to (z pominięciem szczegółów matematycznych) będzie tematem naszego spotkania.
Spotkanie będzie miało formę hybrydową. W celu uczestnictwa wirtualnego prosimy o zapisanie się przez ten formularz: https://forms.gle/4K1MJ7V9JW8MDKmq7 Uwaga, spotkanie wyjątkowo odbywa się o godz. 12.00!